什么是
对于什么是,我们先看看白皮书中的定义:
是 上的代币。它易于使用、gas、并且零租金。
它是基于以太坊的自动代币交换协议,其设计目标是:易用性、高gas利用率、抗审查、零租金。
自动化做市商(AMM)
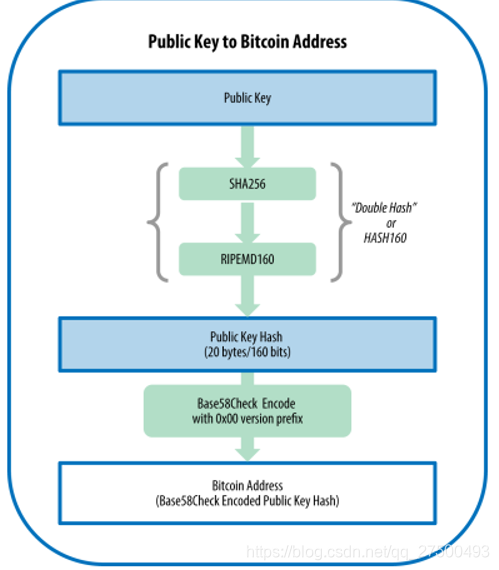
传统交易所有订单簿,记录买卖方向、数量、买入价,交易所负责撮合买卖双方,一旦订单簿中最高价低于或等于最低价,就会促成交易,并产生新的成交价。传统交易所有以下特点:
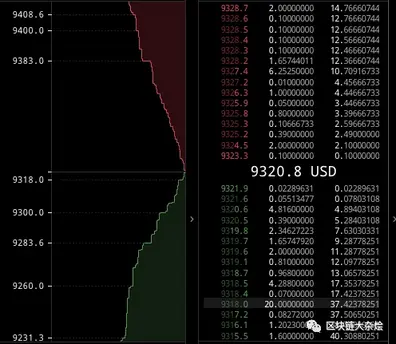
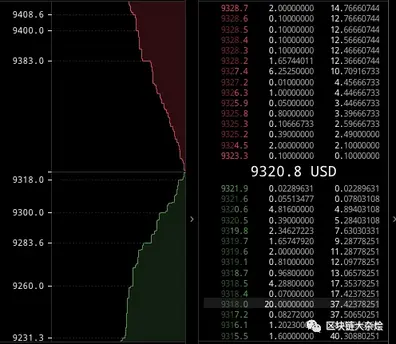
在订单簿模式的市场中,买家期望以最低的价格买入想要的资产,而卖家则期望以最高的价格卖出同一种资产。如果要成交,买卖双方必须就价格达成共识,一是买家提高出价,二是卖家降低出价。如果双方都不愿意改变出价,那就要靠做市商的参与了。简单来说,做市商是一个促成交易的实体,它会在买卖两个方向下订单,这样想要交易的参与者只要匹配做市商的订单就可以完成交易,而不必等待对手方出现后才能交易,这大大提高了市场的流动性。
为什么不采用订单簿模式?
部署在每秒能处理大约 15 笔交易的以太坊上,这对于订单簿交易所来说是不可行的。主要原因是:“订单簿模式依赖一个或多个外部做市商不断为某种资产做市,而以太坊的 TPS 太低,无法支撑做市商的高频交易。如果没有做市商,交易所的流动性会立即下降,这样的交易所的用户体验会很差。”
利用流动性池加常数乘法公式的自动化做市商(AMM)模式实现资产的交换,自动化做市商模式不需要买卖双方下单,也不需要买卖双方重叠订单,可以自由进行买卖。
流动池
流动性池是智能合约中锁定的所有代币和资金的统称。流动性意味着将资金转换成代币,或者将代币转换成资金。
一个完整的流动性池被分成两部分,代表不同的货币,成为交易对。在 V1 中是 ETH 和 ERC20 代币。在 V2 中,它支持不同 ERC20 代币的直接兑换。因此,V2 中的流动性池可以允许两边有不同的 ERC20 代币,ETH 会自动转换成 WETH 代币。为了简单起见,我们将以 ETH-ERC20 交易对为例。
如下图所示,做市商的所有ETH都放在流动性池的左侧,所有的ERC20都放在流动性池的右侧。如果有用户想买入ERC20代币,那么ERC20代币会从流动性池的右侧转给用户,而用户支付的ETH会加入到流动性池的左侧,然后重新计算流动性池中的价格,等待下一次交易。
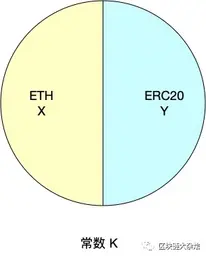
货币本身无法创造,所以需要依赖外部资金为合约提供流动性。为流动性池提供流动性的用户被称为流动性提供者。当流动性提供者向池子注入流动性时,就会铸造出流动性代币(LP),铸造的LP代币数量与用户在流动性池中注入的资金占比有关。流动性提供者可以随时选择销毁自己的流动性代币。为了鼓励用户为流动性池提供更多的流动性,会从总交易金额中抽取0.3%作为交易费,全额支付给那些向资金池注入资金提供流动性的流动性提供者。
常数乘积公式
假设网络中有一个ETH-DAI交易对的流动性池,用户在兑换DAI和ETH时,需要一种方法来确定交易价格。
该定价模型非常简洁,其核心思想是一个常数乘积公式$x×y=k$,其中x和y代表流动性池中两种资产的数量,k是两种资产数量的乘积。
$x×y=k$的函数图像如下:
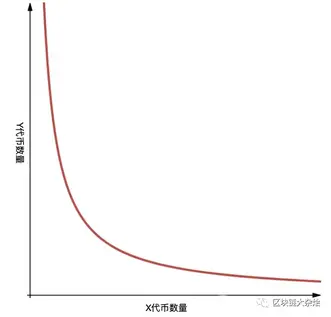
假设乘积 k 为固定常数,当用户使用 x 资产从流动性池中赎回 y 资产时,流动性池中的 x 资产数量将增加,y 资产数量将减少。由于 k 为常数,因此当 x 增加 $\Delta X$ 时,y 需要减少 $\Delta Y$ 才能使等式保持不变。
$(x+\Delta X)× (y-\Delta Y)=k$
这里不考虑手续费的问题,如果要计算手续费的话,公式如下:
$(x+\Delta X \gamma ) × (y-\Delta Y)=k'$
$k' > k$
其中:$\rho =0.3\% $,$\gamma =1- \rho $
$\Delta X \gamma$表示扣除手续费后加入流动性池的资产,由于手续费加入流动性池,所以计算出来的k'会大于k,详细过程后面会推导。
接下来会进行一些数学公式的推导,为了方便理解,我们先对不包含手续费的情况进行推导,包含手续费的推导过程放在最后。
交易价格计算不含手续费
交易价格的计算方式有两种:
$x'=x+\Delta x=(1+ \alpha )x = \frac{1}{1-\beta } x$
$y'=y-\Delta y=\frac{1}{1+\alpha }y=(1-\beta )y$
$xy=x'y'=k$
其中:$\alpha=\frac{\Delta x}{x}$,$\beta =\frac{\Delta y}{y}$
$\Delta x=\alpha x$
$x'=(1+\alpha )x=\frac{1}{1-\beta }x \ 1+\alpha =\frac{1}{1-\beta } \ \alpha =\frac{\beta }{1-\beta }$
$\Delta x=\frac{\beta}{1-\beta }x$
$\Delta y=\frac{\alpha }{1-\alpha }y$
以下是输入价格的函数图:
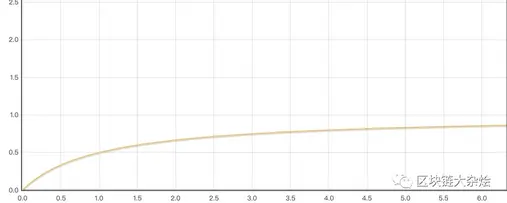
从上图我们可以看到,注入流动性池的$\Delta X$越多,可以从流动性池中取出的$\Delta Y$就越多,但$\Delta Y$只会不断接近流动性池中现有的代币数量,而不会超过它,这意味着你永远不可能一次性把流动性池里的所有代币都买光。可以看出恒等乘积公式可以提供无限的流动性,你想买多少就买多少。
交易滑点
交易滑点指的是:“在买卖$Token$的时候,实际支付的价格与预期成交价格之间的差额称为交易滑点。”
要从流动资金池中购买 $\Delta Y$ Token,需要支付 $\Delta X$,因此此次购买的价格为:$\frac{\Delta X }{\Delta Y }$
$P=\frac{\Delta X }{\Delta Y }=\frac{\alpha x }{\frac{\alpha }{1+\alpha }y}=(1+\alpha)\frac{x}{y}$
$P'=\frac{x}{y}$
$滑点 = PP' = (1+\alpha)P' -P'=\alpha P'$
其中:$P'=\frac{x}{y}$代表当前流动性池中的价格
从公式中我们可以看出,交易的滑点和$\alpha =\frac{\Delta X}{x}$呈线性关系。
下图是滑点的函数图像:
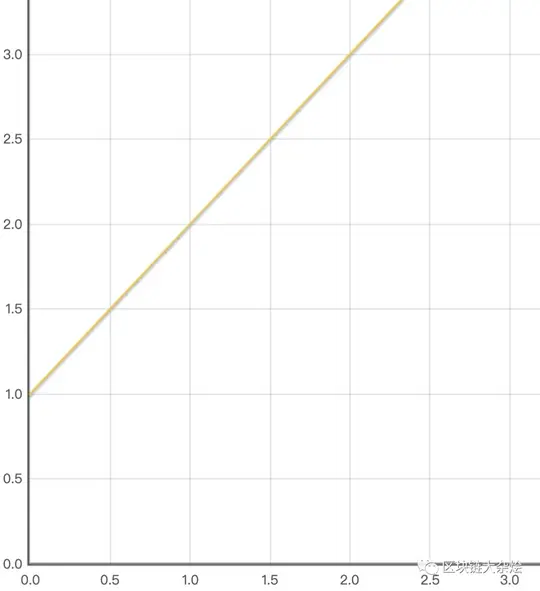
滑点(偏差)取决于$\frac{\Delta X}{x}$,当资金池足够大时,滑点较小。当资金池固定时,一个区块时间内的净交易量越小,滑点就越小。一个区块时间内的净交易量与两个因素有关,一是区块确认速度,二是市场价格波动。因此,恒定产品做市的滑点与以下三个因素高度相关:
流动池币价格
当你从流动性池中购买 $\Delta Y$ 代币时,它肯定会导致当前流动性池的价格波动:
$P=\frac{x' }{y' }=\frac{(1+\alpha) x }{\frac{1 }{1+\alpha }y}=(1+\alpha)(1+\alpha)\frac{x}{y}$
其中:是购买代币后流动性池中货币的价格
从公式中我们可以看出流动性池中货币的价格是二次函数关系
下图是价格的函数图:
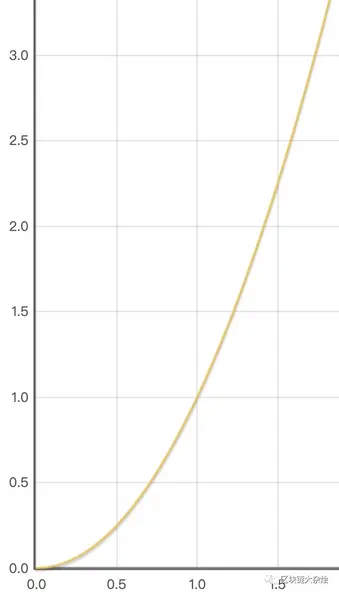
当流动性池中的价格与外部市场价格不一致时,就会出现套利者。套利者会监控全球各地交易所的价格,一旦发现两家交易所的价格有差异,就会两边低买高卖,赚取差价。套利者的存在,让币价不会与全球市场脱节。
床单
对于不太理解以上公式的朋友,可以参考下表的数据,在Excel中手动计算,就能更直观的了解工作原理。
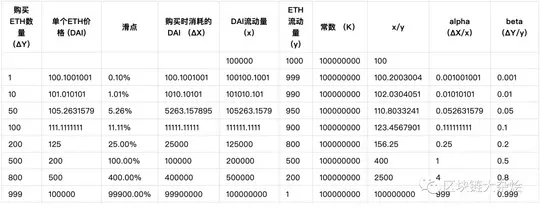
添加手续费常数乘积公式
下面的过程是在计算手续费的情况下,对上面的公式进行重新推导。
计算交易价格
$x'_\rho =x+\Delta x=(1+\alpha )x=\frac{1+\beta (\frac{1}{\gamma }-1)}{1-\beta }x$
$y'_\rho =y+\Delta y=\frac{1}{(1+\alpha \gamma )}y=(1-\beta )y$
$k'>x'\rho y'\rho =(1+\beta (\frac{1}{\gamma }-1))xy>k\ (k'>k 加上手续费后计算)$
除了有交易费时 k 会增加之外,还有一种情况也会导致 k 值发生变化,当向流动性池中添加流动性时,k 会增加,而从流动性池中提取流动性时,k 会减少。具体的变化比例可以参考白皮书,这里就不推导了。
其中:$\alpha = \frac{\Delta x}{x}$,$\beta = \frac{\Delta y}{y}$,$0\leq \rho < 1 $,$\gamma =1-\rho $,当前交易手续费为:$\rho = 0.3\% $
$\Delta x=\frac{\beta}{1-\bata} \cdot \frac{1}{\gamma}\cdot x$
$\Delta y=\frac{\alpha \gamma }{1+\alpha \gamma } \cdot y$
交易滑点
$P=\frac{\Delta
$P'=\frac{x}{y}$
$滑移=PP' = \frac{(1+\alpha \gamma )}{\gamma }\frac{x}{y} -\frac{x}{y}=\frac{1+(\alpha-1)\gamma }{\gamma }\frac{x}{y}$
流动资金池的价格
$\frac{x'\rho }{y'\rho }=\frac{(1+\alpha )x}{\frac{1}{1+\alpha \gamma }y}=(1+\alpha )(1+\alpha \gamma )\frac{x}{y}$
流动资金池的好处和风险
平台内流动性提供者的收入主要来源于交易佣金,每笔交易将收取0.3%的手续费,手续费将按照流动性提供者所占流动性池的比例进行分配。
损失
为流动性池提供流动性的人会发现一个现象:“流动性池中的资金的当前价值小于进入流动性池之前的资金价值,即资金缩水了。”这种现象被称为“损失”。损失在中文里翻译为“无常损失”。简单来说,损失是指你把加密货币放入流动性池所获得的收益与你把加密货币放入钱包所获得的收益之间的差额。公式为:$L={lp}-{bodl}$
Hodl 意味着无论价格如何波动,长期持有某种加密货币(坚持持有)
亏损通常是由流动性池的价格波动引起的。以下是一个例子:
$e × t=k $$p=t/e$$e=\sqrt \frac{k}{p}$$t=\sqrt {k ×p}$
其中:表示流动性池中的 ETH 数量,表示流动性池中的 DAI 数量,表示流动性池中的价格
用户开始向流动性池注入$e=100$,$t=10,000$,当前市场价格为:$p=\frac{t}{e}=100$
$k=et=100*10,000=1,000,000$
假设外部市场价格发生改变,价格变成:$p'=120$。由于价格差异,套利者开始行动。套利者通过移动区块的方式,让流动性池中的价格与外部市场保持一致。此时,流动性池中最新的金额为:
时的资金计算:
计算投入流动性池后的资金:
计算损失:
可以看到,价格从100变成120之后,我们的资金就只有之前的99.59%,损失大概是4%。只要我们此时不从流动性池中提取资金,一旦流动性池中的币价回到100,我们就不会有任何损失。这就是为什么叫无常损失。
下图展示了亏损率和当前价格变化的关系,O列代表资金刚投入流动性池的情况,O->H代表价格上涨时亏损的变化,A<-O代表价格下跌时亏损的变化。
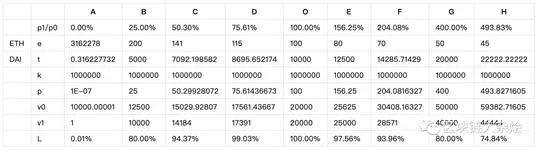
下图是根据以上数据绘制的函数图,蓝色曲线不含手续费,黄色曲线含手续费,红线是我为了方便说明手动添加的。
我们先看蓝色曲线,在不考虑手续费收入的情况下,无论币价涨跌,流动性提供者都会亏损100%。
再看黄色曲线,由于黄色曲线是计算交易费收入的,所以只要币价在一定范围内波动,流动性提供者就能赚取稳定的交易费收入。
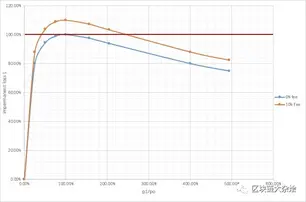
由此我们可以得出一个结论,引入亏损对流动性提供者的影响,可以在两种货币价格波动较小的情况下为流动性池提供流动性。
以下是计算损失的公式
其中:是价格变化率
以下为不计算手续费的衍生流程:
$et=e't'=k$$\frac{e}{t}=P$,$\frac{e'}{t'}=P'$,$\frac{e'}{t'}=\sqrt \frac{P'}{P}$,$\frac{t'}{t}=\sqrt \frac{P}{P'}$,$=\sqrt \frac{P}{P'}$
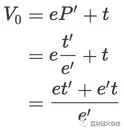
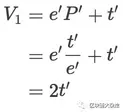
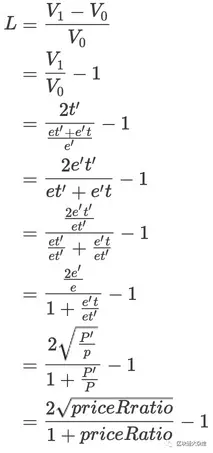
优缺点总结
本文最初发表于: